Tính chu vi, thể tích, diện tích hình lục giác đều là một trong những đề thi kiểm tra được rất nhiều thầy cô đưa vào đề thi. Vì thế ngày hôm nay dapanchuan.com sẽ giúp các bạn hiểu chi tiết hơn về hình lục giác đều. Trước khi tìm hiểu về lục giác đều thì chúng ta nên tìm hiểu về hình lục giác trước nhé.

Vậy Hình lục giác là gì?
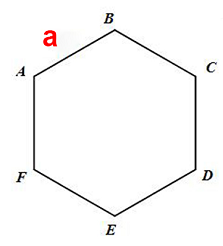
Hình lục giác hay còn gọi hình sáu cạnh tên tiếng Anh là Hexagon. Đây là một đa giác, một hình thể trong hình học phẳng gồm có sáu góc và sáu cạnh.
Hình lục giác là một hình học đặc biệt quan trọng trong cấu trúc hình học, được coi là hình có diện tích quy hoạnh các cạnh nhỏ nhất nhưng lại phủ chứa được lượng khoảng trống lớn nhất và hình lục giác là hình được ứng dụng khá thoáng đãng trong thống kê giám sát trong thực tiễn .
Ngoài ra, hình lục giác đều còn mang những đặc thù sau :
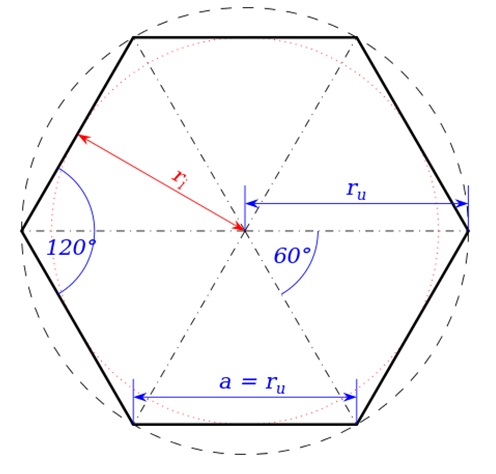
Hình lục giác đều gồm có 6 hình tam giác đều
Bán kính của đường tròn ngoại tiếp sẽ bằng với chiều dài của cạnh lục giác
Các cạnh liền kề nhau trong hình lục giác đều tạo thành 1 góc 120 độ
Hướng dẫn cách vẽ hình lục giác đều đơn giản
Để vẽ được 1 hình lục giác đều bằng compa, bạn hãy triển khai theo các bước sau :
Trước tiên, bạn hãy vẽ 1 đường tròn C có nửa đường kính bất kể
Đặt tâm của compa nằm trên đường tròn C, quay các đường tròn khác đồng tâm với đường tròn C, đỉnh của hình lục giác đều chính là điểm cắt với hình tròn trụ C
Tâm của đường tròn sau là giao điểm của đường tròn C với đường tròn trước đó
Hình lục giác đều là gì?
Hình lục giác đều là hình có tất cả các góc cùng kích thước và các cạnh bằng nhau. Một hình khối với hai đáy hình lục giác gọi là lục lăng. Một hình lục giác với sáu cạnh có chiều dài bằng nhau và các góc có cùng kích thước thì được gọi là lục giác đều.
Đặc điểm hình lục giác đều
– Tổng số đo ở đỉnh là \ ( ( n. 180 ^ { \ circ } – 360 ^ { \ circ } ) = 180 ^ { \ circ }. ( n-2 ) \ ). mà n là số cạnh của đa giác đều. Vậy độ lớn của góc ở đỉnh là : \ ( 180 ^ { \ circ }. \ dfrac { n-2 } { n } \ )
– Các cạnh bằng nhau và các góc ở đỉnh bằng nhau .
– Gọi R và r là nửa đường kính của đường tròn ngoại và nội tiếp của đa giác đều, gọi cạnh của đa giác đều là a, thì ta có : \ ( a = 2. R.sin ( \ dfrac { 360 ^ { \ circ } } { 2 }. n ) = 2.r.tan ( \ dfrac { 360 ^ { \ circ } } { 2 }. n ) \ )
– Các cạnh của nó dài đúng bằng nửa đường kính đường tròn ngoại tiếp .
– Nếu nối tâm đường tròn ngoại ( và nội ) tiếp với các đỉnh của lục giác thì ta sẽ có 6 tam giác đều .
– Tâm của đường tròn ngoại ( và nội ) tiếp là tâm đối xứng quay ( tỏa tròn ) .
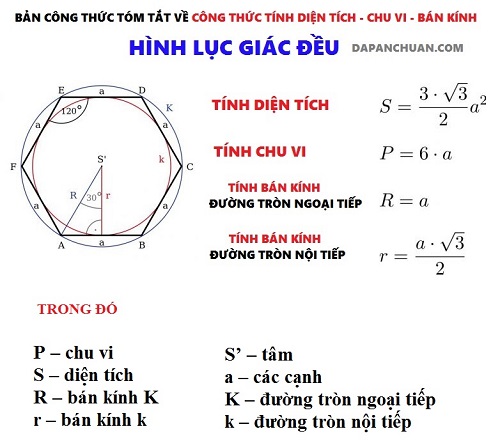
Công thức tính chu vi, thể tích, diện tích hình lục giác đều
Có khá nhiều cách để tính được hình lục giác đều, sau đây chúng tôi sẽ tổng hợp cách tính chi tiết cụ thể nhất về các công thức tính được hình lục giác đều và cũng sẽ tóm gọn lại cho các bạn một cách mạng lưới hệ thống hơn .
Công thúc tính diện tích hình lục giác đều
Công thức tính diện tích quy hoạnh hình lục giác : Muốn tính diện tích quy hoạnh của hình lục giác thường, ta hoàn toàn có thể chia hình lục giác thành 4 hình tam giác, tính tổng diện tích quy hoạnh của các tam giác đó là tìm ra diện tích quy hoạnh của hình lục giác .
Công thức tính diện tích quy hoạnh hình lục giác đều : \ ( S = \ dfrac { 3 \ sqrt3 a ^ 2 } { 2 } \ )
Trong đó:
S là kí hiệu diện tích quy hoạnh .
a là độ dài cạnh của lục giác .
Tính diện tích hình lục giác đều khi biết độ dài một cạnh
Trường hợp đề bài cho sẵn độ dài một cạnh, bạn chỉ cần thay số mà đề bài đã cho vào công thức tính diện tích quy hoạnh \ ( S = \ dfrac { 3 \ sqrt3 a ^ 2 } { 2 } \ )
Trường hợp xác định độ dài qua chu vi (P):
Các bạn học sinh chỉ cần áp dụng công thức tính chu vi hình lục giác đều là P = 6 x a => suy ra tìm a bằng công thức a = P : 6 để tìm cạnh của một hình lục giác đều bất kỳ.
Sau khi xác lập được chiều dài của cạnh các bạn học viên chỉ cần thay vào công thức tính diện tích quy hoạnh hình lục giác đều : \ ( S = \ dfrac { 3 \ sqrt3 a ^ 2 } { 2 } \ ) và tính .
Tính diện tích hình lục giác đều khi biết đường trung đoạn
Trung đoạn là đoạn thẳng vuông góc kẻ từ tâm của lục giác đều đến một cạnh bất kể của nó .
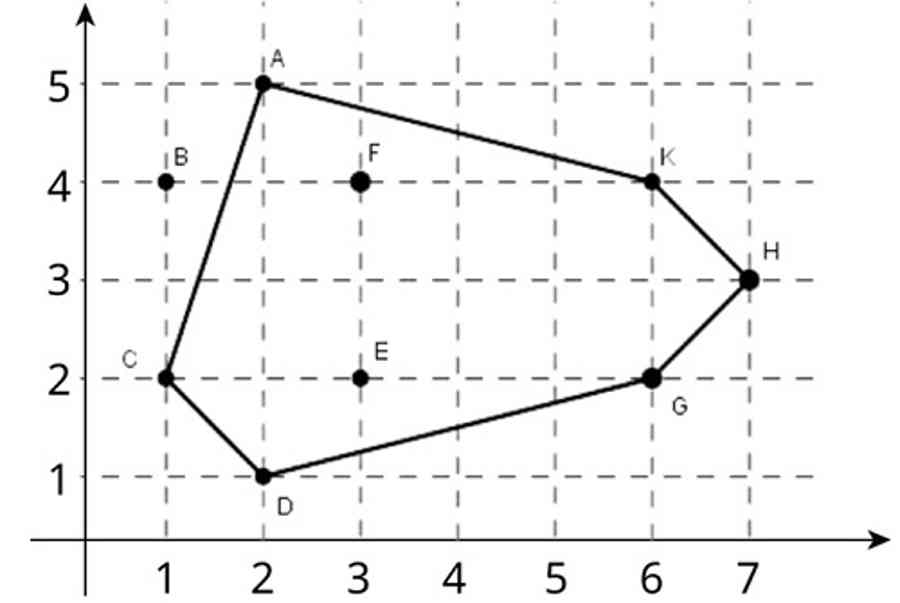
Tính diện tích hình lục giác không đều khi biết các đỉnh
Bước 1: Xác định tọa độ các đỉnh của đa giác không đều.
Bạn hãy xác lập tọa độ của tổng thể các đỉnh lục giác bằng hệ trục tọa độ x, y. Khi biết tọa độ các đỉnh của một hình lục giác thì bạn sẽ thuận tiện tính được diện tích quy hoạnh của nó .
Bước 2: Tạo bảng giá trị tọa độ.
Bạn hãy lập một bảng liệt kê tọa độ x, y của mỗi đỉnh theo thứ tự ngược chiều kim đồng hồ đeo tay và lặp lại giá trị tiên phong ở cuối bảng .
Bước 3: Tính nhóm kết quả (1)
Lấy tọa độ x của đỉnh trước nhân với giá trị y của đỉnh tiếp theo rồi cộng các tích lại với nhau .
 Có thể thông qua việc xác định tọa độ để tính diện tích của lục giác không đều
Có thể thông qua việc xác định tọa độ để tính diện tích của lục giác không đều
Bước 4: Tính nhóm kết quả hai (2)
Ngược với bước 3, tại bước này ta sẽ lấy tọa độ y của đỉnh trước nhân với tọa độ x của đỉnh tiếp theo rồi lấy tổng các tích .
Bước 5: Lấy tổng các tích của nhóm (1) trừ đi tổng các tích của nhóm (2) sau đó lấy trị tuyệt đối của kết quả.
Bước 6: Tính diện tích của lục giác không đều.
Thương của hiệu quả ở bước năm chia cho hai sẽ là diện tích quy hoạnh của lục giác không đều .
Tính chu vi của hình lục giác đều
Công thức tính chu vi của hình lục giác đều: P = 6 x a
Trong đó:
S là kí hiệu chu vi
a là độ dài cạnh của lục giác .
Tính bán kính đường tròn ngoại tiếp của hình lục giác đều
Công thức bán kính tính đường tròn ngoại tiếp của hình lục giác đều : R = a
Trong đó:
R là nửa đường kính đường tròn ngoại tiếp
a là độ dài cạnh của lục giác .
Tính bán kính đường tròn nội tiếp của hình lục giác đều
Công thức tính nửa đường kính đường tròn ngoại tiếp của hình lục giác đều : \ ( r = \ dfrac { a \ sqrt3 } { 2 } \ )
Trong đó:
r là nửa đường kính đường tròn nội tiếp
a là độ dài cạnh của lục giác.
Bảng tóm tắt công thức tính chu vi, thể tích, diện tích hình lục giác đều
Sau đây là bảng tóm tắt về các công thức về hình lục giác đều để ccascc bạn học viên đỡ rối não khi phải thấy quá nhiều sự diễn giải bên trên
Hi vọng với bài viết lần này các bạn đã có thể biết cách tính chu vi, thể tích, diện tích hình lục giác đều rồi nhé. Mong rằng các bạn thấy hữu ích hãy chia sẻ cho các bạn của mình nữa nhé
Source: https://tbdn.com.vn
Category: Toán Học