Tứ giác có thể là tứ giác đơn (không có cặp cạnh đối nào cắt nhau), hoặc tứ giác kép (có hai cặp cạnh đối cắt nhau). Tứ giác đơn có thể lồi hoặc lõm. Và tổng các góc của một tứ giác luôn là 360 độ.
- Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác. Đặc điểm của tứ giác lồi là tất cả các góc trong nó đều nhỏ hơn 180° và hai đường chéo đều nằm bên trong tứ giác
- Còn tứ giác lõm luôn tồn tại ít nhất một cạnh mà đường thẳng chứa cạnh đó chia cắt tứ giác thành hai phần.
Hôm nay tất cả chúng ta sẽ cùng nhau khám phá về cách tính chu vi của tứ giác, cũng như cách tính diện tích của một tứ giác bất kể, các tứ giác đặc biệt quan trọng, tứ giác ngoại tiếp đường tròn và tứ giác nội tiếp đường tròn ..
I. Công thức tính chu vi và diện tích tứ giác bất kỳ
Bạn đang đọc: Công thức tính DIỆN TÍCH TỨ GIÁC và CHU VI TỨ GIÁC
Chu vi của một tứ giác bất kể bằng tổng độ dài bốn cạnh .
Công thức: $C_{ABCD}=AB+BC+CD+DA$
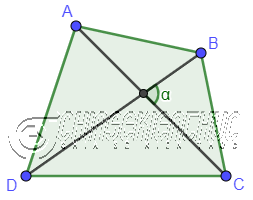
Diện tích của một tứ giác bất kể bằng ½ tích của độ dài đường chéo thứ nhất, độ dài đường chéo thứ 2 và sin của góc tạo bởi hai đường chéo đó .
Công thức: $S_{ABCD}=\frac{1}{2}.AC.BD.\sin\alpha$ với $\alpha$ là góc tạo bởi hai đường chéo.
II. Công thức tính chu vi và diện tích của tứ giác đặc biệt
Trong phạm vi của bài viết này mình sẽ trình bày với các bạn công thức tính chu vi và diện tích của năm tứ giác đặc biệt thường gặp, đó là: hình thang, hình bình hành, hình chữ nhật, hình thoi và hình vuông.
Các trường hợp còn lại bạn nếu có nhu yếu bạn hoàn toàn có thể tự điều tra và nghiên cứu thêm trên Internet và SGK nhé .
#1. Công thức tính diện tích tứ giác
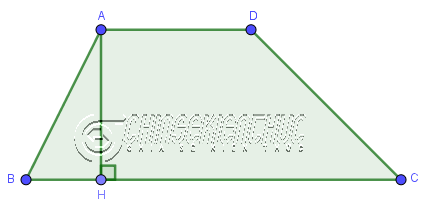
Diện tích của hình thang bằng ½ tích của tổng hai cạnh đáy và chiều cao
Công thức: $S_{ABCD}=\frac{1}{2}.(AD+BC).AH$
#2. Công thức tính chu vi tứ giác
Chu vi của hình thang bằng tổng độ dài của bốn cạnh
Công thức: $C_{ABCD}=AB+BC+CD+DA$
#3. Công thức tính diện tích hình bình hành

Diện tích của hình bình hành sẽ bằng tích của độ dài một cạnh và độ dài chiều cao tương ứng .
Công thức: $S_{ABCD}=BC.AH$
#4. Công thức tính chu vi hình bình hành
Chu vi của hình bình hành bằng hai lần tổng độ dài hai cạnh liên tục .
Công thức: $C_{ABCD}=2.(AB+AD)$
#5. Công thức tính diện tích hình chữ nhật

Diện tích của hình chữ nhật sẽ bằng tích của độ dài hai cạnh liên tục .
Công thức: $S_{ABCD}=AB.AD$
#6. Công thức tính chu vi hình chữ nhật
Chu vi của hình chữ nhật bằng hai lần tổng độ dài hai cạnh liên tục .
Công thức: $C_{ABCD}=2.(AB+AD)$
#7. Công thức tính diện tích hình thoi
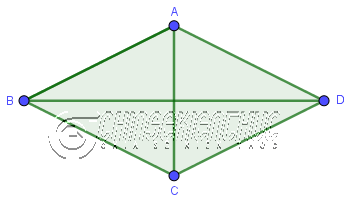
Diện tích của hình thoi bằng ½ tích của độ dài đường chéo thứ nhất với độ dài đường chéo thứ 2 .
Công thức: $S_{ABCD}=\frac{1}{2}.AC.BD$
#7. Công thức tính chu vi hình thoi
Chu vi của hình thoi bằng bốn lần độ dài của một cạnh .
Công thức: $C_{ABCD}=4.AB$
#8. Công thức tính diện tích hình vuông
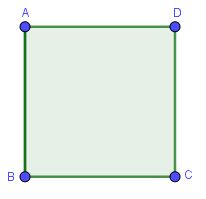
Diện tích của hình vuông vắn sẽ bằng bình phương độ dài một cạnh .
Công thức: $S_{ABCD}=AB^2$
#9. Công thức tính chu vi hình vuông
Chu vi của hình vuông vắn bằng bốn lần độ dài của một cạnh .
Công thức: $C_{ABCD}=4.AB$
III. Công thức tính Chu vi và Diện tích tứ giác nội tiếp đường tròn
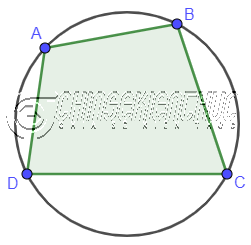
Chu vi của tứ giác ABCD nội tiếp đường tròn tâm O bằng tổng độ dài bốn cạnh .
Diện tích của tứ giác ABCD nội tiếp đường tròn tâm O bằng
USD \ sqrt { ( p-AB ) ( p-BC ) ( p-CA ) ( p-DA ) } $ với p là nửa chu vi của tứ giác ABCD và p được tính theo công thức $ \ frac { AB + BC + CD + DA } { 2 } $
Chú ý: Tâm của đường tròn ngoại tiếp tứ giác nếu có trong nhiều trường hợp không phải là giao điểm của hai đường chéo.
IV. Công thức tính Chu vi và Diện tích tứ giác ngoại tiếp đường tròn
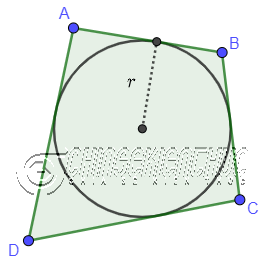
Chu vi của tứ giác ABCD ngoại tiếp đường tròn tâm O bằng tổng độ dài bốn cạnh
Diện tích của tứ giác ABCD ngoại tiếp đường tròn tâm O bằng USD p. r USD với p là nửa chu vi của tứ giác ABCD, r là độ dài nửa đường kính đường tròn nội tiếp
Chú ý: Tâm đường tròn nội tiếp tứ giác nếu có sẽ trùng với giao điểm của bốn đường phân giác trong
V. Lời kết
Như vậy là mình đã trình bày với các bạn đầy đủ về tất cả các công thức tính chu vi tứ giác và công thức diện tích của tứ giác rồi nhé.
Từ tứ giác thường thì đến tứ giác rất đặc biệt quan trọng, từ tứ giác nội tiếp đến tứ giác ngoại tiếp .
Nói chung là dựa vào những công thức trong bài viết này thì bạn hoàn toàn có thể tính được chu vi và diện tích của một tứ giác bất kể .
Công thức tiên phong trong bài viết cũng là công thức chung hoàn toàn có thể vận dụng cho mọi tứ giác, các công thức tiếp theo đều được biến hóa dựa theo các yếu tố đặc biệt quan trọng về cạnh, về góc của tứ giác sao cho dễ vận dụng nhất .
Hi vọng bài viết này sẽ có ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm :
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Bài viết đạt : 5/5 sao – ( Có 1 lượt nhìn nhận )
Source: https://tbdn.com.vn
Category: Toán Học


