Hình trụ tròn là hình có hai mặt đáy là hai hình tròn trụ song song với nhau và bằng nhau. Ta hoàn toàn có thể thấy rất nhiều hình tròn trụ được sử dụng trong trong thực tiễn hoàn toàn có thể kể đến như : lon sữa bò, cốc uống nước, lọ hoa, thùng đựng nước, … Hình trụ được sử dụng khá thông dụng trong thực tiễn do đó cách tính thể tích hình tròn trụ cũng được vận dụng rất nhiều trong thực tiễn. Để hoàn toàn có thể tính được thể tích hình tròn trụ thì bài viết dưới đây là một trong những bài viết mà các em không nên bỏ lỡ .

THỂ TÍCH KHỐI TRỤ

Để tính thể tích khối trụ, ta lấy chiều cao nhân với bình phương độ dài của nửa đường kính hình tròn trụ ở dưới mặt đáy hình tròn trụ và số pi .V = π. r2. h

 

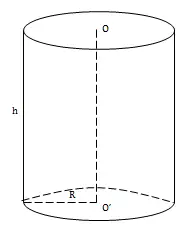Trong đó :V là thể tích khối trụ có đơn vị chức năng là mét khối ( m3 )r là nửa đường kính hình tròn trụ ở mặt dưới khối trụh là chiều cao của khối trụπ là hằng số pi ( π = 3, 14 )

BÀI TẬP VẬN DỤNG

Bài 1: Tính thể tích của khối trụ biết khoảng cách giữa hai tâm đáy là a (cm) và đường kính của đáy là b(cm)

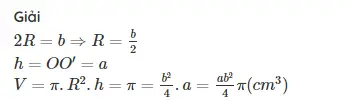
Bài 2: Cho hình chữ nhật ABCD có AC = 10cm, AB=6cm. Cho đường gấp khúc ABCD quay quanh AD ta được 1 hình trụ. Tính thể tích khối trụ được giới hạn bởi hình trụ trên.

Bài 3: Cho một hình trụ bất kỳ có bán kính mặt đáy r = 4 cm, trong khi đó, chiều cao nối từ đỉnh của hình trụ xuống đáy hình trụ có độ dài h = 8 cm. Hỏi thể tích của hình trụ này bằng bao nhiêu ?

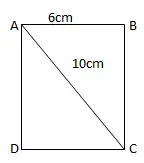
Bài giải :Bán kính dưới mặt đáy hình tròn trụ r = 4 cm, chiều cao hình tròn trụ h = 8 cm. Áp dụng công thức tính thể tích hình tròn trụ ta được hiệu quả như sau :V = π x r2 x h = π x 42 x 8 = ~ 402 cm3Bài 4 : Cho hình tròn trụ có đáy là hai hình tròn trụ tâm O và O ’, nửa đường kính đáy bằng 2. Trên đường tròn đáy tâm O lấy dây cung AB = 2. Biết rằng thể tích khối tứ diện OO’AB là 8. Tính thể tích khối trụ .Giải :

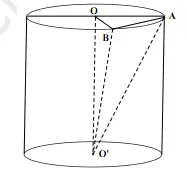
Tam giác OAB có OA = OB = AB = 2SOAB =Tam giác OAB có OA = OB và OO ’ vuông góc với ( OAB )Suy ra OO ’

Vậy thể tích hình tròn trụ là :

Bài 5 : Cho hình tròn trụ có nửa đường kính đáy x, chiều cao y, diện tích quy hoạnh toàn phần bằng. Với giá trị x nào thì hình tròn trụ sống sót ? Tính thể tích V của khối trụ theo x và tìm giá trị lớn nhất của VĐáp án : hình tròn trụ sống sót khi 0 < x < 1

Bài 6 : Bên trong hình tròn trụ có một hình vuông vắn ABCD cạnh a tiếp nối đuôi nhau mà A, B thuộc đường tròn đáy thứ nhất và C, D thuộc đường tròn đáy thứ 2 của hình tròn trụ, mặt phẳng hình vuông vắn tạo với đáy hình tròn trụ một góc 450. Tính thể tích khối trụ

Bài 7 : Cho một hình lăng trụ đứng ABCA1B1C1 có ABC là tam giác vuông. AB = AC = a ;

AA1 = a . M là trung điểm AA1. Tính thể tích hình lăng trụ MA1BC1

Bài 8 : Cho hình lăng trụ ABCA’B ’ C ’ có đáy là tam giác đều cạnh a, cạnh bên AA ’ = b. Tam giác BAC ’ và tam giác B’AC là các tam giác vuông tại Aa ) Chứng minh rằng : Nếu H là trọng tâm của tam giác A’B ’ C ’ thì AH vuông góc với ( A’B ’ C ’ )b ) Tính VABCA’B ’ C ’Đáp án

Bài 9 : Cho hình tròn trụ có đáy là đường tròn tâm O và O ’ tứ giác ABCD là hình vuông vắn nội tiếp trong đường tròn tâm O, AA ’, BB ’ là các đường sinh của khối trụ. Biết góc của mặt phẳng ( A’B ’ CD ) và đáy hình tròn trụ bằng 600. Tính thể tích khối trụĐáp số :

Bài 10: Một hình trụ có diện tích toàn phần  . Xác định các kích thước của khối trụ để thể tích của khối trụ này lớn nhất

Đáp số : Vmax khi R = 1, h = 2Bài 11 : Cho hình tròn trụ có 2 đáy là 2 đường tròn tâm O và O ’, nửa đường kính đáy bằng r, chiều cao bằng h. Hai điểm A, B lần lượt đổi khác trên 2 đường tròn đáy sao cho độ dài AB = d không đổi ( d > h ) .a ) Tính thể tích của tứ diện OO’AB theo r, h, d .b ) Chứng minh rằng : khoảng cách giữa 2 đường thẳng AB và OO ’ không đổi

Bài 12: Cho hình lăng trụ ABCA’B’C’ có độ dài cạnh bên bằng 2a, tam giác ABC là tam giác vuông tại A, AB = a,  Hình chiếu vuông góc của A’ trên (ABC) là trung điểm BC. Tính VA’ABC theo a ?

Đáp án : VA’ABC = a3 / 2

 

Source: https://tbdn.com.vn
Category: Toán Học