Đồng quy là một dạng bài mà chúng ta thường gặp trong Toán hình học cấp 2 cũng như cấp 3. Vậy đồng quy là gì? Làm thế nào để chứng minh được 3 đường thẳng đồng quy? Trong nội dung bài viết dưới đây, maynenkhikhongdau.net sẽ giúp bạn tổng hợp kiến thức về chủ đề này nhé!
Đồng quy là gì?
Trước khi khám phá 3 đường thẳng đồng quy là gì tất cả chúng ta hãy cùng xem qua lý giải thế nào là đồng quy nhé ! Đồng quy thực ra là một từ Hán Việt nhưng được sử dụng khá nhiều trong đời sống hàng ngày .
- Đồng : Có nghĩa là cùng nhau, song hành, sát cánh
-
Quy: Có nghĩa là tụ lại, tập trung, tập hợp tại một điểm
Bạn đang đọc: Đồng quy là gì? Cách chứng minh 3 đường thẳng đồng quy
Nói Tóm lại “ đồng quy ” tức là cùng gặp nhau tại một vị trí đơn cử.
Ba đường thẳng đồng quy là gì?
Định nghĩa về ba đường thẳng đồng quy được diễn giải như sau : “ Cho ba đường thẳng lần lượt là a, b, c không trùng với nhau. Nếu ba đường thẳng a, b, c cùng đi qua một điểm O nào đó thì ta sẽ gọi đó là đồng quy .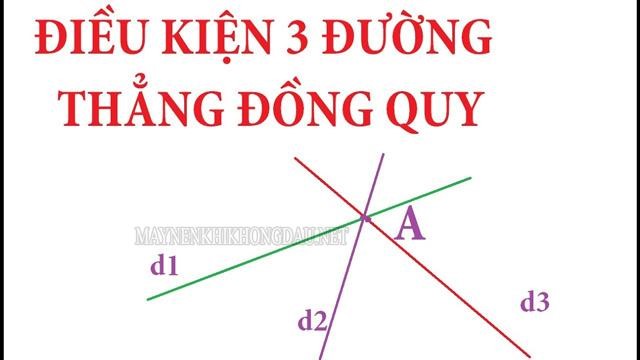
Đường đồng quy sẽ có những tính chất nổi bật gì?
Dưới đây là một số ít đặc thù vô cùng quan trọng về đường đồng quy mà bạn cần ghi nhớ để hoàn toàn có thể ứng dụng vào quy trình làm bài tập .– Nếu hai đường cao của tam giác cắt nhau tại một điểm đơn cử thì từ đó hoàn toàn có thể suy ra đường cao thứ 3 cũng sẽ cùng đi qua giao điểm đó .– Nếu ba đường trung tuyến của một tam giác đồng quy tại 1 điểm thì điểm này sẽ được gọi là trọng tâm của tam giác .– Ba đường cao trong một tam giác đồng quy tại 1 điểm thì điểm này sẽ được gọi là trực tâm của tam giác .– Nếu hai đường trung tuyến trong tam giác bất kể cắt nhau tại một điểm thì từ đó ta hoàn toàn có thể suy ra đường trung tuyến thứ 3 chắc như đinh cũng đi qua giao điểm đó. Trọng tâm sẻ chia đoạn thẳng trung tuyến thành 3 phần : Từ trọng tâm lên tới đỉnh chiếm tới 2/3 độ dài của trung tuyến đó .– Nếu ba đường phân giác trong một tam giác đồng quy tại 1 điểm đơn cử thì điểm này sẽ được gọi là tâm của đường tròn nội tiếp tam giác .– Nếu hai đường phân giác của tam giác cắt nhau tại một điểm đơn cử thì từ đó ta hoàn toàn có thể suy ra đường phân giác thứ 3 cũng sẽ đi qua giao điểm đó. Giao điểm của 3 đường phân giác sẽ cách đều 3 cạnh của tam giác .– Khi ba đường trung trực trong một tam giác đồng quy tại 1 điểm thì điểm này sẽ được gọi là tâm đường tròn ngoại tiếp tam giác .– Nếu hai đường trung trực bên trong tam giác cắt nhau tại một điểm thì từ đó tất cả chúng ta hoàn toàn có thể suy ra đường trung trực thứ 3 chắc như đinh đi qua giao điểm đó. Giao điểm của 3 đường trung trực sẽ cách đều 3 đỉnh của tam giác .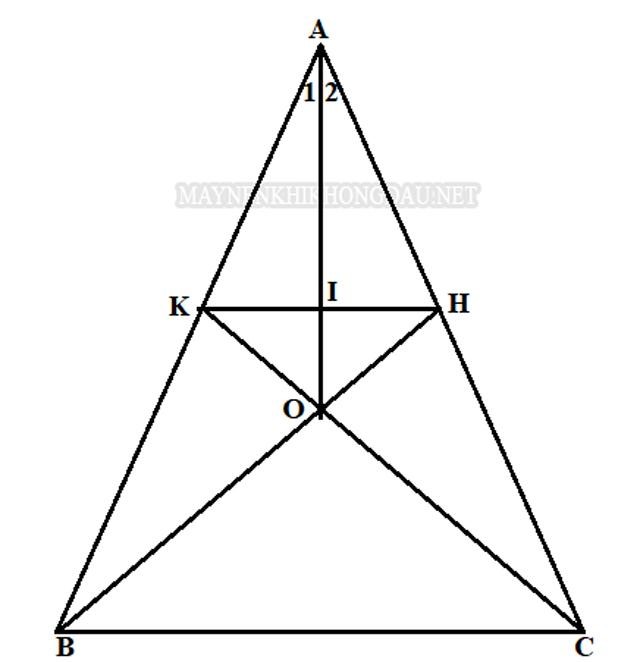
Hướng dẫn cách chứng minh đồng quy trong toán học
Để chứng minh 3 đường thẳng đồng quy bạn hoàn toàn có thể vận dụng những cách làm sau đây :Cách 1 : Tìm giao điểm của hai đường thẳng, sau đó triển khai chứng minh đường thẳng thứ ba cũng đi qua giao điểm đó .Cách 2 : Chứng minh một điểm bất kể cũng thuộc vào ba đường thẳng đó .Cách 3 : Sử dụng 1 trong những đặc thù đồng quy trong tam giác như thể :* Ba đường thẳng có chứa những đường trung tuyến .* Ba đường thẳng có chứa những đường phân giác .* Ba đường thẳng có chứa những đường trung trực .* Ba đường thẳng có chứa những đường những đường cao .Cách 4 : Sử dụng đặc thù của những đường thẳng định ra trên hai đường thẳng song song và những đoạn thẳng tỉ lệ .Cách 5 : Sử dụng những chứng minh phản chứng .
Cách 6: Sử dụng tính chất thẳng hàng của các điểm
Cách 7 : Chứng minh những đường thẳng đều đi qua một điểm duy nhất .
Luyện tập giải các bài tập liên quan đến 3 đường thẳng đồng quy
Dưới đây là một số ít bài tập thường gặp về đường thẳng đồng quy mà bạn hoàn toàn có thể tìm hiểu thêm :
Bài 1: Cho tam giác ABC, qua lần lượt mỗi đỉnh A, B, C ta kẻ 3 đường thẳng song song với cạnh đối diện và chúng sẽ cắt nhau tại F, D, E. Hãy chứng minh rằng ba đường thẳng AD, BE, CF đồng quy tại 1 điểm.
Lời giải:
Ta có :AE / / BCAB / / CETừ đó suy ra được ABCE là 1 hình bình hành .⇒ AE = BCDùng cách chứng minh tương tự như ta cũng có ACBF là hình bình hành .⇒ AF = BC⇒ AE = AFNhư vậy A là trung điểm của EF .Tương tự ta cũng có được B là trung điểm của đường thẳng DF, C là trung điểm của DE .Như vậy, A, B, C lần lượt là trung điểm của ba cạnh tam giác DEF. Do đó ta hoàn toàn có thể ⇒ AD, BE, CF đồng quy tại trọng tâm của tam giác DEF .
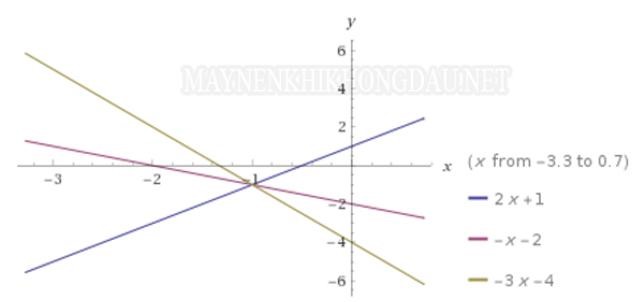
Bài 2: Tìm m để 3 đường thẳng sau đồng quy tại 1 điểm.
Ta có 3 đường thẳng lần lượt là ( d1 ) : y = 2 x + 1 ; ( d2 ) : y = ( – x ) – 2 ; ( d3 ) : y = ( m-1 ) x – 4
Lời giải:
Xét phương trình hoành độ là giao điểm của đường thẳng ( d1 ) và ( d2 ) ta có : y = 2 x + 1 = ( – x ) – 2 ⇔ 3 x = – 3 ⇔ x = – 1Suy ra ta có y = 2 x ( – 1 ) + 1 = – 1Như vậy giao điểm của ( d1 ) với ( d2 ) sẽ là là I ( – 1 ; – 1 )
Để ba đường thẳng trên đồng quy thì điểm I sẽ phải thuộc vào đường thẳng (d3)
=> – 1 = ( m – 1 ) x ( – 1 ) – 4 ⇔ m = – 2Như vậy phương trình đường thẳng ( d3 ) sẽ là : y = – 3 x – 4Hy vọng bài viết trên của chúng tôi đã giúp bạn hiểu đường đồng quy là gì, đặc thù của nó cũng như cách chứng minh để hoàn toàn có thể giải bài tập tương quan một cách nhanh gọn nhất nhé !
Source: https://tbdn.com.vn
Category: Toán Học