Cách chứng minh hình bình hành? Tính chất của hình bình hành? Hình bình hành là hình gì? Hôm nay Vimi sẽ chia sẻ với các bạn học sinh “bí kíp” làm dạng bài này nắm chắc điểm 10 trong tay.
1. Hình bình hành là gì?
📌 Hình bình hành tên tiếng anh là Parallelogram là một hình thang có dạng đặc biệt với hai cạnh bên song song. Hay còn gọi là một tứ giác có các cạnh đối song song với nhau. Đây là một dạng hình học thông dụng thường xuất hiện trong lĩnh vực toán học và kỹ thuật hiện nay.
2. Dấu hiệu nhận biết cơ bản của hình bình hành
Hình bình hành có một số tính chất cơ bản như:
Bạn đang đọc: 5 Cách chứng minh hình bình hành? Dấu hiệu nhận biết
✔ Các cặp cạnh đối song song và bằng nhau .
✔ Các góc trong hình đối nhau và bằng nhau .
✔ Tại trung điểm mỗi đường, 2 đường chéo cắt nhau, gọi là tâm đối xứng của hình bình hành .
2.1. Khi bạn cần chứng minh 1 hình tứ giác là hình bình hành
Khi đề bài cho một hình tứ giác, hãy nhìn vào những tín hiệu dưới đây để nhận ra hình bình hành :
✔ Có hai cặp cạnh đối nhau, song song và bằng nhau .
✔ Có hai cạnh của tứ giác đối nhau, song song và bằng nhau .
✔ Có hai cặp góc của hình tứ giác đối nhau và bằng nhau .
✔ Hai đường chéo của tứ giác cắt nhau tại trung điểm mỗi đường .
2.2. Khi hình bình hành tồn tại ở dạng hình thang
Khi đề bài cho một hình thang, hãy nhìn vào những tín hiệu dưới đây để phân biệt hình bình hành :
✔ Khi hình thang có cặp cạnh đáy bằng nhau .
✔ Khi hình thang có cặp cạnh hai bên song song với nhau .
Với những tín hiệu đó, tất cả chúng ta sẽ thuận tiện liên tưởng đến những hình như : hình chữ nhật, hình vuông vắn, hình thoi – đó là những hình dạng đặc biệt quan trọng của hình bình hành. Chỉ cần bám sát vào những tín hiệu sẽ rất dễ để nhận ra .
3. Cách chứng minh hình bình hành
Khi chứng minh một tứ giác là hình bình hành, tiên phong những bạn cần nắm chắc những tín hiệu nhận ra của hình bình hành. Vì đó là những yếu tố quan trọng mà tất cả chúng ta sẽ bám sát trong quy trình làm bài. Hoặc tất cả chúng ta sẽ sử dụng dạng đặc biệt quan trọng, chứng minh hình thang sau đó trải qua những tín hiệu của hình bình hành trong hình thang để chứng minh .
3.1. Chứng minh tứ giác là hình bình hành khi có 2 cặp cạnh đối song song
✔ Cho hình bình hành ABCD. Có AB / / DC và AD / / BC < => ABCD là hình bình hành ( theo đặc thù những cặp cạnh đối song song với nhau ) .
3.2. Chứng minh tứ giác là hình bình hành khi có 2 cặp cạnh đối bằng nhau
✔ Cho tứ giác ABCD. 2 đường chéo AC và BD cắt nhau tại O. Có tam giác ABC và tam giác ADC :
- AD = BC
- AB = CD
✔ Trong đó, cạnh chung giữa hai tam giác là AC => Tam giác ABC = tam giác ADC ( theo đặc thù cạnh. cạnh. cạnh )
✔ Khi hai tam giác bằng nhau, ta có :
- Góc BAC = góc DAC ( góc tương ứng ). 2 góc này ở vị trí so le trong => BC / / AD ( 1 )
- Góc CAB = góc ACD ( góc tương ứng ). 2 góc này ở vị trí so le trong => DC / / AB ( 2 )
✔ Từ ( 1 ) và ( 2 ), ta có tứ giác ABCD là hình bình hành .
3.3. Chứng minh tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành
✔ Từ định nghĩa, đặc thù của hình bình hành, ta có :
- AB / / CD
- AB = CD
- AI = IB
- DK = KC
=> AI / / KC và AI = KC
3.4. Chứng minh tứ giác có 2 cặp góc đối bằng nhau là hình bình hành
✔ Cho tứ giác ABCD có tam giác ABD = tam giác BCD và tam giác ABC = tam giác ADC .
✔ Ta có :
- Tam giác BCD = tam giác BAD ( theo kim chỉ nan ) => góc BCD = góc BAD ( 1 )
- Tam giác ABC = tam giác ADC ( theo kim chỉ nan ) => góc ABC = góc ADC ( 2 )
✔ Từ ( 1 ) và ( 2 ), do những góc đối bằng nhau nên ta chứng minh được tứ giác ABCD là hình bình hành .
3.5. Chứng minh tứ giác có hai đường chéo cắt nhau tại trung điểm là hình bình hành
✔ Tứ giác ABCD có AC cắt BD tại O => O là trung điểm của AC và BD .
Ta có OA = OC và OB = OD .
✔ Xét tam giác AOD và tam giác COB có:
- OA = OC
- Góc AOD = góc BOC ( đối đỉnh )
- OB = OD
=> tam giác AOD = tam giác COB ( theo đặc thù cạnh – góc – cạnh )
- => AD = BC ( 1 ) .
- Góc DAO = góc BCO => AD / / BC ( 2 )
✔ Từ ( 1 ) và ( 2 ) => tứ giác ABCD là hình bình hành .
4. Các dạng bài tập về hình bình hành
Hình bình hành có những dạng bài từ cơ bản đến nâng cao. Để làm được những bạn học viên cần nắm vững triết lý cũng như đặc thù của hình bình hành, làm thuần thục những dạng bài cơ bản trước .
Dạng 1: Ứng dụng tính chất của hình bình hành để chứng minh các tiên đề liên quan
✔ Phương pháp : Bám sát vào kim chỉ nan nhận ra tín hiệu trong hình bình hành về góc, cạnh, đường chéo, những đặc thù song song và bằng nhau từ đó chứng minh được những đặc thù hình học khác .
Dạng 2: Chứng minh một tứ giác là hình bình hành
✔ Phương pháp : Sử dụng ngặt nghèo những tín hiệu phân biệt trong hình và những hình dạng đặc biệt quan trọng của hình bình hành để chứng minh .
Dạng 3: Chứng minh 3 đường thẳng đồng quy, 3 điểm thẳng hàng.
✔ Phương pháp : Áp dụng những đặc thù về đường chéo và tâm đối xứng của hình bình hành .
=> Dù là dạng cơ bản hay nâng cao cũng yên cầu người làm có nền tảng kỹ năng và kiến thức vững chãi để thuận tiện vận dụng và chứng minh lan rộng ra .
5. Cách tính chu vi, diện tích hình bình hành
Bạn đọc hoàn toàn có thể tìm hiểu thêm cách tính chu vi và tính diện tích quy hoạnh hình bình hành ngay dưới đây :
5.1. Chu vi hình bình hành
✔ Chu vi một hình bình hành sẽ bằng C = (a+b) x 2 (tức là 2 lần tổng của một cặp cạnh bất kỳ kề nhau), (C là kí hiệu chu vi).
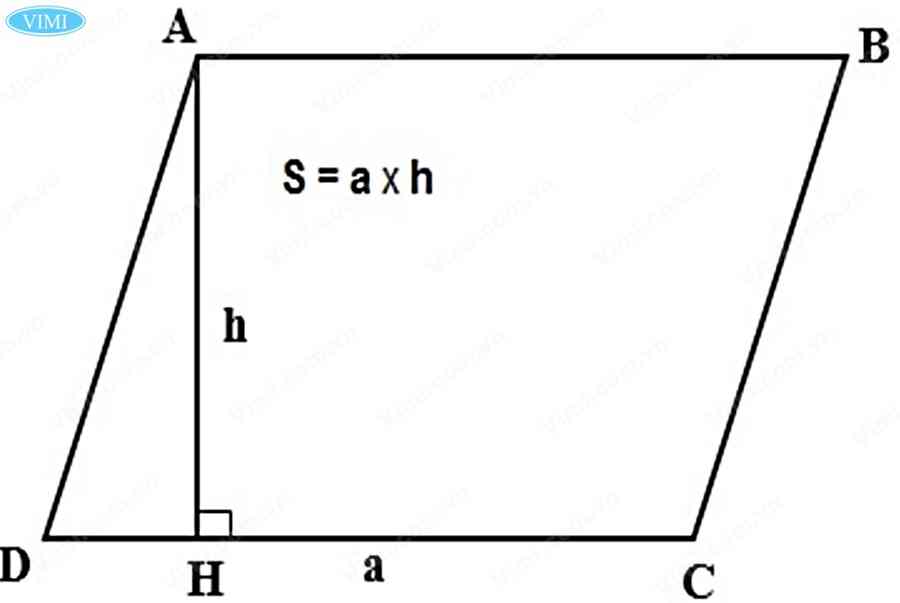
5.2. Diện tích hình bình hành
✔ Diện tích một hình bình hành sẽ bằng S = B x H trong đó:
-
B là độ dài cạnh đáy.
-
H là độ dài của chiều cao.
-
S là kí hiệu diện tích.
6. Một số lưu ý khi chứng minh hình học
Bất cứ một loại hình học nào cũng có những tín hiệu và đặc thù riêng không liên quan gì đến nhau. Chỉ cần nắm chắc những tín hiệu này sẽ giúp cho bạn làm những bài tập hình học đơn thuần và nhanh gọn hơn nhiều .
✔ Khi nhìn thấy đề bài, hãy tập thói quen vẽ hình, phác thảo hình ảnh theo đề sẽ giúp bạn tưởng tượng một cách nhanh gọn hơn phương hướng giải .
✔ Khi vẽ được hình là bạn đã xử lý được 50 % bài toán, sau đó hãy dựa vào những kỹ năng và kiến thức triết lý nhận biết dạng hình học và những đặc thù tương quan giúp bạn chứng minh .
✔ Đừng học triết lý một cách máy móc và giải đề một cách cứng ngắc, hãy coi kim chỉ nan là nền tảng và linh động, phát minh sáng tạo trong giải pháp giải sẽ giúp bạn giải được những dạng bài tập khác nhau .
✔ Hãy học cách chứng minh khoa học, khá đầy đủ những bước dựa trên hình vẽ sao cho người đọc nhìn vào cảm thấy dễ hiểu, thoải mái và dễ chịu. Viết tắt quá nhiều hay làm quá sơ sài sẽ khiến bài của bạn bị trừ điểm đấy !
Chúc các bạn giành được những điểm số cao trong học tập!
5
/
5
(
1
bầu chọn
)
Source: https://tbdn.com.vn
Category: Toán Học
