Tính chất, dấu hiệu nhận biết và cách chứng minh hình vuông lớp 8
Khái niệm, những đặc thù cũng như cách nhận ra hình vuông và cách chứng minh hình vuông học viên đã được khám phá trong chương trình Toán 8, phân môn Hình học. Nhằm giúp những em nắm vững hơn phần Hình học 8 vô cùng quan trọng này, THPT Sóc Trăng đã san sẻ bài viết sau đây. Các em theo dõi nhé ! Ở đây, chúng tôi đã mạng lưới hệ thống lại toàn bộ những kỹ năng và kiến thức cần ghi nhớ và giải pháp chứng minh hình vuông cực hay .
I. LÝ THUYẾT VỀ HÌNH VUÔNG CẦN GHI NHỚ
Bạn đang đọc: Tính chất, dấu hiệu nhận biết và cách chứng minh hình vuông lớp 8 – Trường THPT Thành Phố Sóc Trăng
1. Định nghĩa
Bạn đang xem : Tính chất, tín hiệu nhận ra và cách chứng minh hình vuông lớp 8
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau .
Tổng quát: ABCD là hình vuông

Nhận xét:
+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau .
+ Hình vuông là hình thoi có bốn góc vuông .
+ Hình vuông vừa là hình chữ nhật vừa là hình thoi .
2. Tính chất
Trong một hình vuông có :
- Hai đường chéo bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.
- Có 2 cặp cạnh song song.
- Có 4 cạnh bằng nhau.
- Có một đường tròn nội tiếp và ngoại tiếp đồng thời tâm của cả hai đường tròn trùng nhau và là giao điểm của hai đường chéo của hình vuông.
- Một đường chéo sẽ chia hình vuông thành hai phần có diện tích bằng nhau.
- Giao điểm của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm.
3. Dấu hiệu nhận biết hình vuông
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông .
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông .
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông .
+ Hình thoi có một góc vuông là hình vuông .
+ Hình thoi có hai đường chéo bằng nhau là hình vuông .

II. CÁC CÁCH CHỨNG MINH HÌNH VUÔNG HAY NHẤT
Để chứng minh một tứ giác là hình vuông, những em hoàn toàn có thể vận dụng một trong 3 cách sau đây :
1. Cách 1: chứng minh tứ giác là hình vuông theo dấu hiệu hình thoi có 1 góc vuông
Phương pháp: Để chứng minh tứ giác là hình vuông theo dấu hiệu hình thoi có 1 góc vuông ta thực hiện như sau:
- Chứng minh tứ giác đó là hình thoi.
- Chứng minh tứ giác đó có 1 góc vuông.
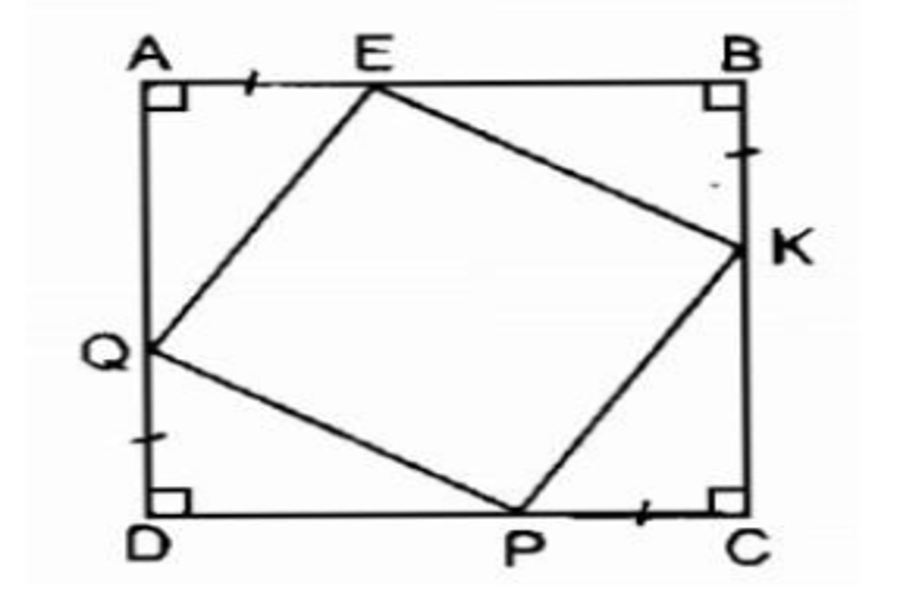
Ví dụ : Cho hình vuông ABCD. Trên AB, BC, CD, DA lấy theo thứ tự những điểm E, K, P., Q. sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì ? Vì sao ?

Ta có : AB = BC = CD = DA ( gt )
AE = BK = CP = DQ ( gt )
=> EB = KC = PD = QA
Xét ΔAEQ và ΔBKE, ta có :
AE = BK ( gt )
A = B = 90 °
QA = EB ( chứng minh trên )
=> ΔAEQ = ΔBKE ( c. g. c )
=> EQ = EK
Chứng minh tương tự như, ta có : EK = KP, KP = PQ
Suy ra : EK = KP = PQ = EQ => Tứ giác EKPQ là Hình thoi. ( 1 )
Mặt khác : ΔAEQ = ΔBKE
⇒ Góc AQE = BKE
Mà Góc AQE + AEQ = 90 °
=> Góc BKE + AEQ = 90 °
Lại có, Góc BKE + QEK + AEQ = 180 °
Suy ra : Góc QEK = 180 ° – Góc BKE – Góc AEQ = 180 ° – 90 ° = 90 ° ( 2 )
Từ ( 1 ) và ( 2 ) suy ra tứ giác EKPQ là Hình vuông ( Hình thoi có 1 góc vuông là Hình vuông. ( đpcm )
2. Cách 2: chứng minh tứ giác là hình vuông theo dấu hiệu hình chữ nhật có 2 cạnh kề bằng nhau
Phương pháp: Để chứng minh tứ giác là hình vuông theo dấu hiệu hình chữ nhật có 2 cạnh kề bằng nhau ta thực hiện như sau:
- Chứng minh tứ giác đó là hình chữ nhật.
- Chứng minh tứ giác đó có 2 cạnh kề bằng nhau.
Ví dụ : Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy những điểm H, G sao cho bh = HG = GC. Qua H và G kẻ những đường vuông góc với BC chúng cắt AB, AC theo thứ tự ở E và F. Tứ giác EFGH là hình gì ? Vì sao ?

Theo bài ra, ta có :
ΔABC vuông cân tại A => Góc B = C = 45 °
ΔBHE vuông tại H và có Góc B = 45 ° => ΔBHE vuông cân tại H
=> HB = HE
ΔCGF vuông tại G và có Góc C = 45 ° => ΔCGF vuông cân tại G
=> GC = GF
Mà Bảo hành = HG = GC ( giả thiết )
=> HE = HG = GF
Lại có EH / / GF ( cùng vuông góc với BC ) và EH = GF
=> Tứ giác HEFG là Hình bình hành ( Tứ giác có một cặp cạnh đối song song bằng nhau là Hình bình hành ).
Ngoài ra, Góc EHG = 90 ° nên HEFG là Hình chữ nhật, lại có EH = HG ( chứng minh trên ) .
Vậy HEFG là Hình vuông ( Hình chữ nhật có 2 cạnh kề bằng nhau là Hình vuông ). ( đpcm )
3. Cách 3: chứng minh tứ giác là hình vuông theo dấu hiệu hình chữ nhật có đường chéo là phân giác
Phương pháp: Để chứng minh tứ giác là hình vuông theo dấu hiệu hình chữ nhật có đường chéo là phân giác ta thực hiện như sau:
- Chứng minh tứ giác đó là hình chữ nhật.
- Chứng minh tứ giác đó có đường chéo là đường phân giác của một góc.
Ví dụ : Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N là chân đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông .

Xét tứ giác AMDN, ta có :
Góc MAN = 90 ° ( giả thiết )
DM ⊥ AB ( giả thiết ) => Góc AMD = 90 °
Doanh Nghiệp ⊥ AC ( giả thiết ) => Góc AND = 90 °
Suy ra Tứ giác AMDN là Hình chữ nhật ( tứ giác có ba góc vuông )
Lại có đường chéo AD là đường phân giác của A
Vậy Hình chữ nhật AMDN là Hình vuông
III. BÀI TẬP CHỨNG MINH HÌNH VUÔNG
Bài 1: Cho hình chữ nhật ABCD có AB = 2AD. Gọi P, Q lần lượt là trung điểm của AB, CD.
a. Chứng minh tứ giác APQD và PBCQ là hình vuông
b. Gọi H là giao điểm của AQ và DP. Gọi K là giao điểm của CP và BQ. Chứng minh PHQK là hình vuông
Bài 2: Cho hình chữ nhật MNRS có MN = 2MS. Gọi P, Q lần lượt là trung điểm của MN;SR.
a. Chứng minh tứ giác MPQS và PNRQ là hình vuông
b. Gọi H là giao điểm của MQ và SP. Gọi K là giao điểm của RP và NQ. Chứng minh PHQK là hình vuông
Bài 3: Cho hình chữ nhật ABCD có AB = 10cm và AD = 5cm. Gọi P, Q lần lượt là trung điểm của AB, CD.
a. Chứng minh tứ giác APQD và PBCQ là hình vuông
b. Gọi H là giao điểm của AQ và DP. Gọi K là giao điểm của CP và BQ. Chứng minh PHQK là hình vuông
Bài 4: Cho tam giác ABC vuông tại A. Đường phân giác AD. Gọi M, N theo thứ tự là chân đường vuông góc hạ từ D đến AB, AC.
a. Chứng minh AMDN là hình vuông
b. Gọi P. đối xứng với D qua M. Chứng minh ADBP là hình thoi
c. NMPA là hình bình hành
Bài 5: Cho tam giác EFK vuông tại E. Đường phân giác ED. Gọi M, N theo thứ tự là chân đường vuông góc hạ từ D đến EF, EK.
a. Chứng minh EMDN là hình vuông
b. Gọi P. đối xứng với D qua M. Chứng minh EDFP là hình thoi
c. NMPE là hình bình hành
Bài 6: Cho tam giác ABC vuông tại A. Đường phân giác AD. Gọi M, N theo thứ tự là chân đường vuông góc hạ từ D đến AB, AC.
d. Chứng minh AMDN là hình vuông
e. Gọi P. đối xứng với D qua M. Tính độ dài DP biết AC = 10 cm
f. NMPA là hình bình hành
Bài 7: Cho hình thang vuông ABCD có góc A bằng góc D và cùng bằng 90. AB = 3cm, AD = 8cm. CD = 5cm. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi K là hình chiếu của M trên CD. Chứng minh MNDK là hình vuông
Bài 8: Cho hình thang vuông ABCD có góc A bằng góc D và cùng bằng 90. AB = 6cm, AD = 16cm. CD = 10cm. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi K là hình chiếu của M trên CD. Chứng minh MNDK là hình vuông
Bài 9: Cho hình vuông ABCD. Lấy các điểm E, F theo thứ tự thuộc các cạnh CD, DA, sao cho AF = DE. Chứng minh AE = BF. Và AE vuông góc BF
Bài 10: Cho hình vuông ABCD. Lấy các điểm E, F theo thứ tự là trung điểm của các cạnh CD, DA. Chứng minh AE = BF. Và AE vuông góc BF
Bài 11: Cho hình vuông ABCD. Lấy các điểm của M, N, P, Q theo thứ tự thuộc các cạnh AB, BC, CD, DA sao cho AM = BN = CP = DQ Tứ giác MNPQ là hình gì? Vì sao ?
Bài 12: Cho tam giác ABC. Điểm M thuộc BC. Qua M dựng đường thẳng song song với AB cắt AC tại D, Qua M dựng đường thẳng song song với AC cắt AB tại E
a. Tứ giác ADME là hình gì ? Vì sao
b. Tìm điều kiện kèm theo của tam giác ABC để tứ giác ADME là hình chữ nhật
Bài 13: Cho tam giác ABC vuông tại A. Điểm M thuộc BC. Qua M dựng đường thẳng song song với AB cắt AC tại D, Qua M dựng đường thẳng song song với AC cắt AB tại E
c. Tứ giác ADME là hình gì ? Vì sao
d. Tìm điều kiện kèm theo của tam giác ABC để tứ giác ADME là hình vuông
Bài 14:Cho vuông ở A, trung tuyến AM. Gọi I là trung điểm của AB, N là điểm đối xứng với M qua I
a. Các tứ giác ANMC, AMBN là hình gì ? Vì sao ?
b. Cho AB = 4 cm ; AC = 6 cm. Tính diện tích quy hoạnh tứ giác AMBN
c. Tam giác vuông ABC có điều kiện kèm theo gì thì AMBN là hình vuông
Bài 15: Cho tứ giác ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD và DA.
a. Chứng minh MNPQ là hình bình hành .
b. Hai đường chéo AC và BD của tứ giác cần có thêm điều kiện kèm theo gì để MNPQ là hình chữ nhật, hình thoi, hình vuông
Bài 16: Cho DABC vuông tại A, AB = 5cm, AC = 12cm, AM là trung tuyến.
a. Tính độ dài BC, AM .
b. Trên tia AM lấy điểm D đối xứng với A qua M. Chứng minh AD = BC. Tam giác vuông ABC cần có thêm điều kiện kèm theo gì thì ABDC là hình vuông
Vậy là các em vừa được ôn tập và hệ thống lại phần kiến thức hình vuông về khái niệm, tính chất, dấu hiệu nhận biết và cách chứng minh hình vuông lớp 8 cực hay. Hãy lưu lại để xem thêm các bạn nhé ! Xem thêm cách chứng minh hình thang tại đường link này bạn nhé !
Đăng bởi : trung học phổ thông Sóc Trăng
Chuyên mục : Giáo dục đào tạo
Source: https://tbdn.com.vn
Category: Toán Học