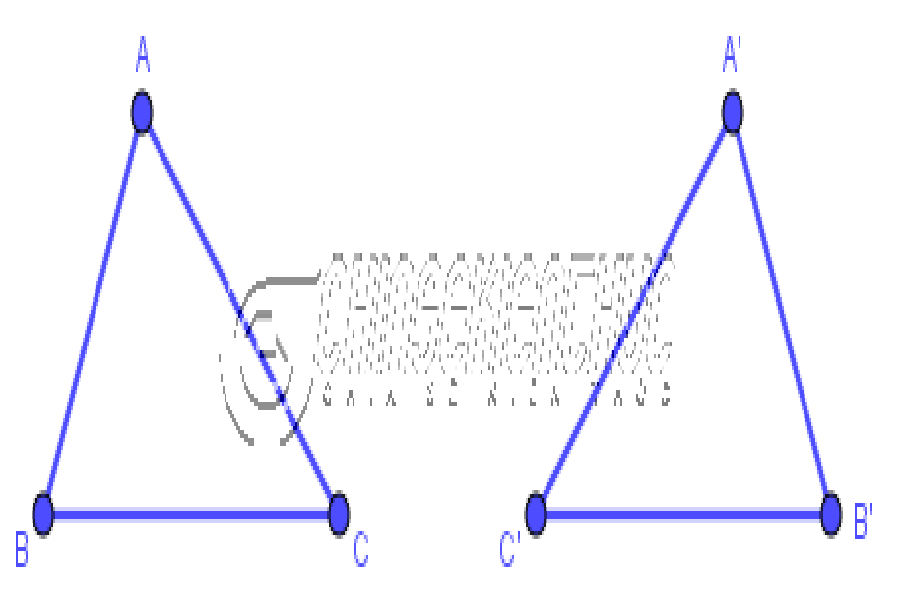
Và để liên tục mạch kiến thức và kỹ năng này thì thời điểm ngày hôm nay tất cả chúng ta sẽ cùng nhau khám phá về ba trường hợp bằng nhau của hai tam giác .
Việc chứng minh hai tam giác bằng nhau có nhiều ứng dụng trong Toán học, tiêu biểu vượt trội nhất là hoàn toàn có thể gián tiếp chứng minh được những cạnh, những góc tương ứng bằng nhau .
I. Hai tam giác bằng nhau là hai tam giác như thế nào?
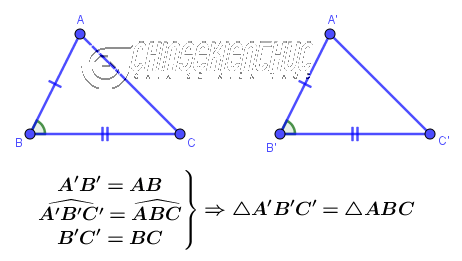
Nếu tam giác này có ba cạnh và ba góc lần lượt bằng ba cạnh và ba góc của tam giác kia thì hai tam giác đã cho bằng nhau.
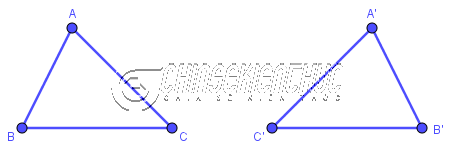
Vì USD AB = A’B ’, BC = B’C ’, CA = C’A ’
Ví dụ 1: Cho
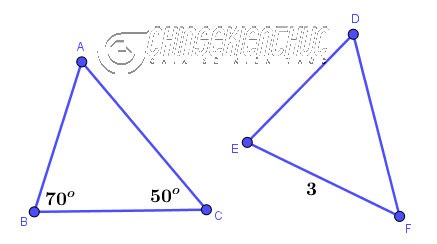
Lời Giải :
USD \ Leftrightarrow \ hat { A } + 70 ^ o + 50 ^ o = 180 ^ o USD
USD \ Leftrightarrow \ hat { A } + 120 ^ o = 180 ^ o USD
Suy ra
Vậy số đo của
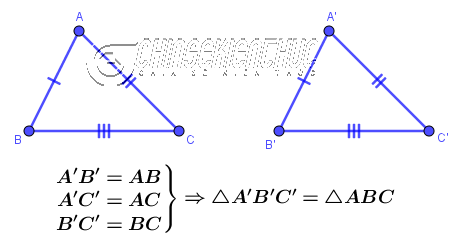
#1. Chứng minh 2 tam giác bằng nhau (Cạnh – Cạnh – Cạnh)
Nếu ba cạnh của tam giác này lần lượt bằng ba cạnh của tam giác kia thì hai tam giác đã cho bằng nhau .
Ví dụ 2: Cho tứ giác ABCD có
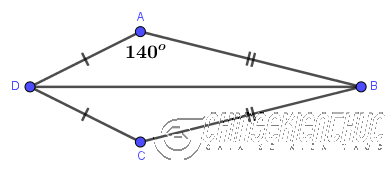
Lời Giải :
Xét
- DC là cạnh chung
Suy ra
Suy ra
#2. Chứng minh 2 tam giác bằng nhau (Cạnh – Góc – Cạnh)
Nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đã cho bằng nhau .
Ví dụ 3: Cho tứ giác ABCD có
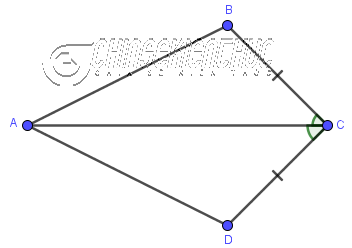
Lời Giải :
Xét
Vậy
Ví dụ 4: Cho tứ giác
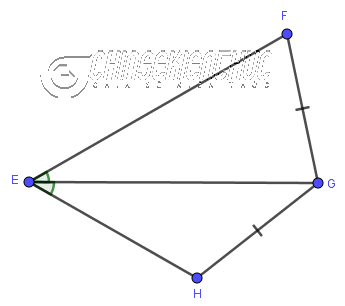
Lời Giải:
Xem thêm: THỂ TÍCH KHỐI TRỤ
Câu vấn đáp là : Không bằng nhau !
Tuy
Giả sử tất cả chúng ta có
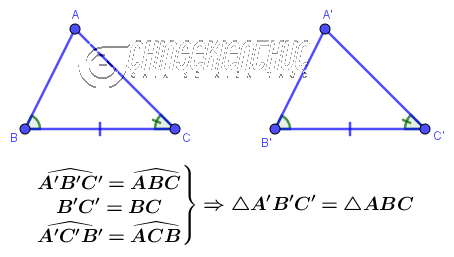
#3. Chứng minh 2 tam giác bằng nhau (Góc – Cạnh – Góc)
Nếu một cạnh và hai góc kề của tam giác này lần lượt bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đã cho bằng nhau .
Ví dụ 5: Tam giác ABC có bằng tam giác DEF hay không? Vì sao?
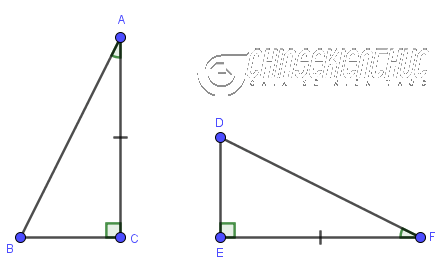
Lời Giải :
Tam giác ABC bằng tam giác DEF
Vì …
Ví dụ 6: Tam giác GHI có bằng tam giác JKL hay không? Vì sao?
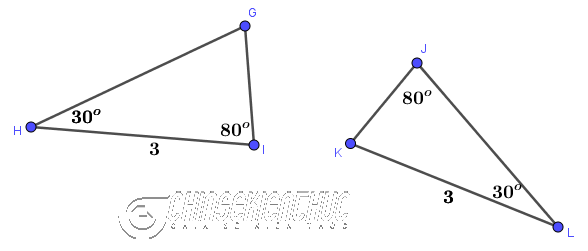
Lời Giải :
Câu vấn đáp : Hai tam giác trên không bằng nhau .
Vì …
- HI có hai góc kề là
- KL có hai góc kề là
Giả sử
II. Lời kết
Vâng, trên đây là 3 cách để chứng minh 2 tam giác bằng nhau, đây là những cách chứng minh đơn giản và được sử dụng nhiều nhất trong hình học.
Hai tam giác bằng nhau thì sẽ có ba cạnh tương ứng bằng nhau, ba góc tương ứng bằng nhau, diện tích quy hoạnh bằng nhau, …
Tuy nhiên điều ngược lại trong nhiều trường hợp hoàn toàn có thể không đúng, thật vậy hai tam giác có ba góc bằng nhau hoàn toàn có thể không bằng nhau, …
Ngoài ra, những bạn cần quan tâm khi chứng minh theo trường hợp thứ 2 và thứ 3 thì góc phải là góc xen giữa, cạnh phải là cạnh xen giữa nha những bạn. Xin chào tạm biệt và hẹn gặp lại những bạn trong những bài viết tiếp theo !
Đọc thêm :
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Bài viết đạt : 5/5 sao – ( Có 1 lượt nhìn nhận )
Source: https://tbdn.com.vn
Category: Toán Học