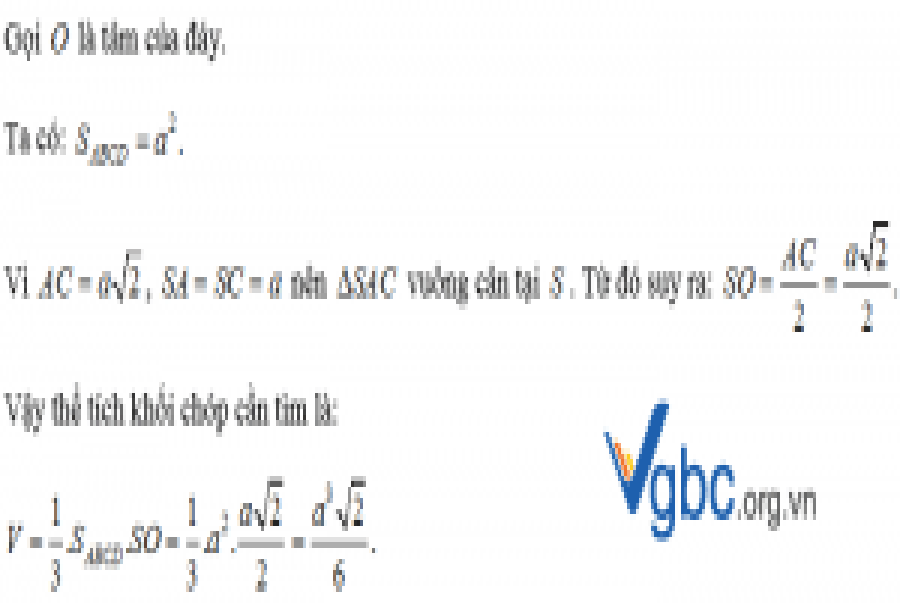Thể tích khối chóp, khối lăng trụ, khối nón và khối trụ được tính theo công thức nào? Đây là câu hỏi nhiều bạn băn khoăn nhất. Dưới đây là cách tính thể tích khối chóp và những ví dụ cụ thể.
Phương pháp tính thể tích khối chóp
Công thức tính thể tích khối chóp: V=13B.h, trong đó B là diện tích đáy, h là chiều cao của khối chóp.
Để tính thể tích khối chóp S.A1A2…An ta đi tính đường cao và diện tích đáy. Khi xác định chân đường cao của hình chóp cần chú ý:
• Hình chóp đều thì chân của đường cao là tâm của đáy.
• Hình chóp có mặt bên (SAiAk) vuông góc với mặt đáy thì chân đường cao của tam giác SAiAk hạ từ S là chân đường cao của hình chóp.
• Nếu có hai mặt phẳng đi qua đỉnh và cùng vuông góc với đáy thì giao tuyến của hai mặt phẳng đó vuông góc với đáy.
• Nếu các cạnh bên của hình chóp bằng nhau thì hình chiếu của đỉnh là tâm đường tròn ngoại tiếp đáy.
• Nếu các mặt bên tạo với đáy một góc bằng nhau thì hình chiếu của đỉnh là tâm đường tròn nội tiếp đáy.
Những ví dụ đơn cử
Tính thể tích khối chop có cạnh bên vuông góc với đáy
Dạng toán này còn hoàn toàn có thể được cho dưới dạng cho hai mặt bên cùng vuông góc với đáy. Khi đó chiều cao của khối chóp chính là giao tuyến của hai mặt đó .

Xem ngay : 1 feet bằng bao nhiêu mm, cm, m, km ? để biết được công thức đúng chuẩn
Ví dụ 1 :
Cho khối chóp S.ABC có đáy là tam giác đều cạnh a. Cạnh bên SA vuông góc với dưới mặt đáy. Tính thể tích khối chóp S.ABC biết cạnh bên SC tạo với mặt dưới góc 60 º .
Lời giải :

Nhận xét : Bài toán đã biết đường cao là SA nhưng chưa biết độ dài. Ta đã biết góc của 1 cạnh bên với đáy. Vì vậy góc đó để tính độ cao. Đáy là tam giác đều đã biết độ dài cạnh. Do đó sẽ tính được diện tích quy hoạnh đáy .
Tính thể tích khối chóp có mặt bên vuông góc với đáy
Đối với khối chóp xuất hiện bên ( SAB ) vuông góc với đáy thì đường cao của hình chóp là SH. Trong đó H thuộc đường thẳng AB. Và yếu tố của tất cả chúng ta thường là phải xác lập vị trí điểm H. Thông thường điểm H là 1 điểm đặc biệt quan trọng nằm trên đường AB. Còn trong trường hợp tất cả chúng ta không xác lập được điểm H thì tất cả chúng ta hoàn toàn có thể vận dụng các hệ thức lượng trong tam giác để tính độ dài SH .
Ví dụ 2 :

Cho khối chóp S.ABCD có đáy là hình vuông vắn cạnh a. Mặt bên ( SAD ) vuông góc với đáy. Biết tam giác SAD vuông cân tại S. Tính thể tích khối chóp A.ABCD.
Lời giải :
Gọi H là trung điểm AD .
Vì tam giác SAD cân tại S nên SH ⊥ AD .
Vì mặt phẳng ( SAD ) vuông góc với đáy nên SH ⊥ ( ABCD ) .
Vì tam giác SAD vuông cân tại S nên :
Vậy thể tích khối chóp cần tìm là:
Tính thể tích khối chóp đều
Khối chóp đều là khối chóp có đáy là đa giác đều và hình chiếu của đỉnh lên mặt đáy trùng với tâm của đáy. Nếu đáy là tam giác đều thì tâm thường xác lập là trọng tâm tam giác. Tứ giác đều chính là hình vuông vắn và tâm là giao hai đường chéo. Thường người ta cũng chỉ xoay quanh hai kiểu đáy tam giác và tứ giác thôi .
Ví dụ 3 :
Tính thể tích khối chóp tứ giác đều có toàn bộ các cạnh bằng a .
Lời giải :

Trên đây là cách tính thể tích khối chóp và những ví dụ đơn cử cho các trường hợp. Hy vọng bài viết của chúng tôi đã cung ứng cho bạn nhiều thông tin .
Rate this post
Source: https://tbdn.com.vn
Category: Toán Học